In many areas of programming, it is important to establish a common
definition of terminology in order to develop clear definitions and to enable a
mutual exchange on existing problems.
In this case, we would like to deal with the terms
of sequence, order and sorting, which developed complex meaning in their
everyday use, and to make them clear in Java, particularly with regard to
collections.
Note:
The definitions used in this article may come into conflict with those in the
literature. This is due to the aforementioned complexity of meanings in their
everyday use, so that other authors understand them in a different way.
Nevertheless, the choice of the author made here should seem directly obvious.
In general, as mentioned above, it is mainly important to agree on common
terminology.
(Fixed) sequence
By a (fixed) sequence of a collection an ordered, reproducible iteration is meant. In other words, iteration over a collection always leads to the same result with the same order.
For example, if the strings “Collections”, “are” and “great!” were stored in a collection, then a collection type with (fixed) sequence returns each time
| Collections are great! |
during complete iteration, while without (fixed) sequence
| great! Collections are | great! are Collections | are great! Collections |
| are Collections great! | Collections great! are |
would be possible as well.
Of course, the cause of an existent or
non-existent (fixed) sequence are the different structures of the different
collection types. This will be illustrated below by means of various linkage
types of LEGO bricks.
Note:
The drawings only illustrate the data structure and say little about other
basic properties.

List (ArrayList, Vector,…)
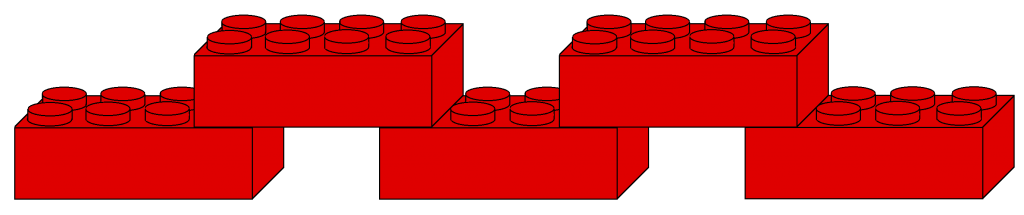
Linked (LinkedMap, LinkedList, LinkedHashMap,…)

Queue / Deque
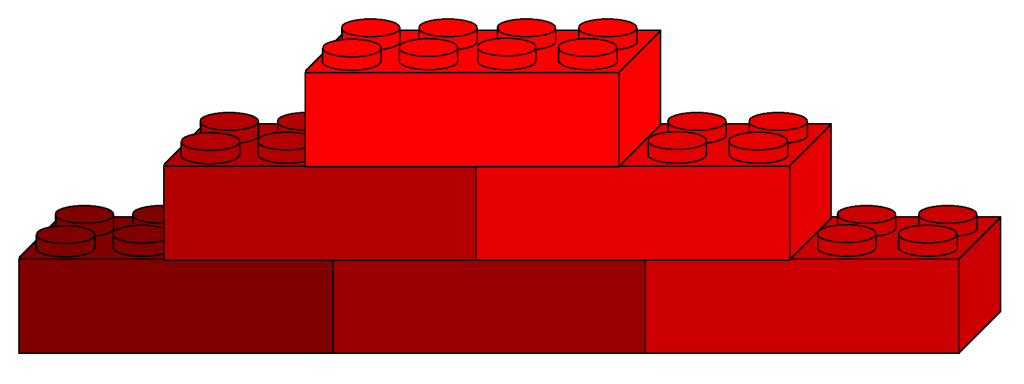
Tree (TreeSet, TreeMap)
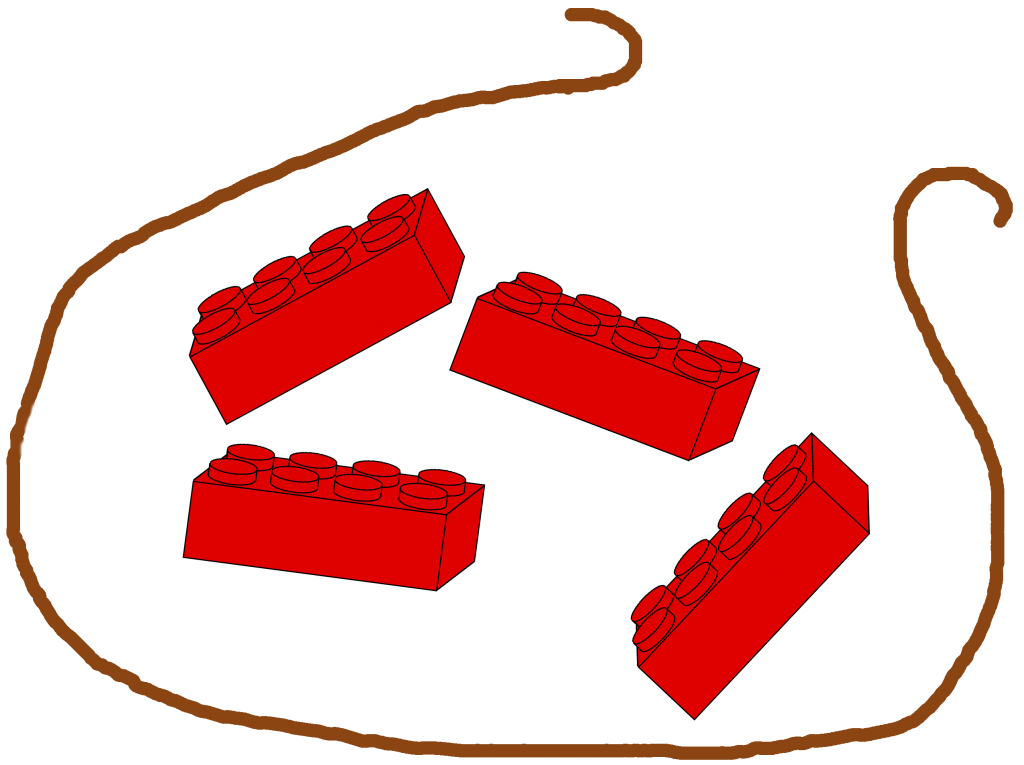
Set (HashSet, not Linked/Tree)
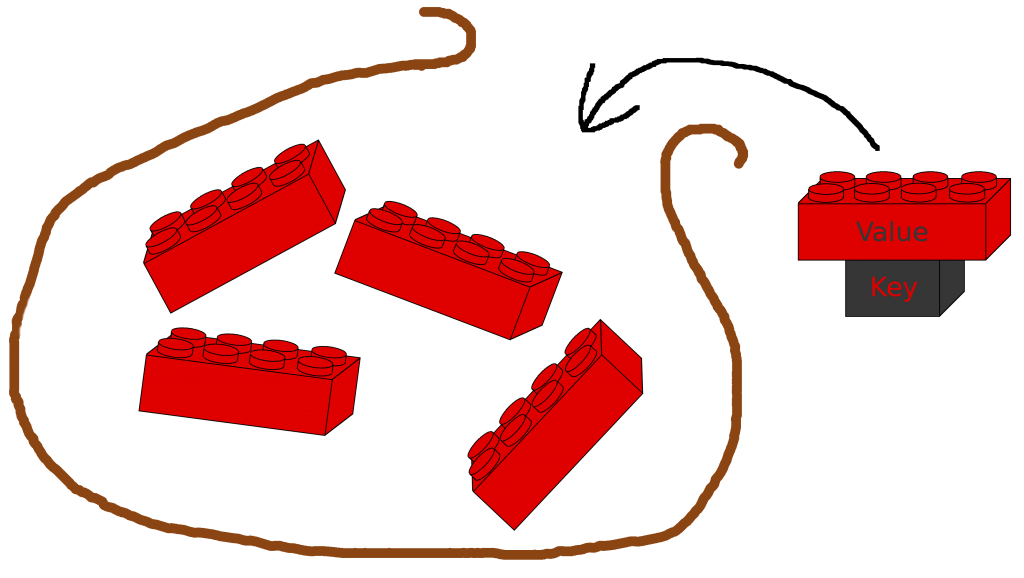
Map ( HashMap, HashTable, not Linked/Tree)
As can be guessed from the illustration, all lists (via the index), linked
collections (chaining with previous and next following element), queues /
deques (stack structure) and tree collections have a structure that allows a
fixed, reproducible iteration and therefore produces a (fixed) sequence.
Sets and maps, on the other hand, can only
guarantee that all elements are read out, but the iteration happens randomly.
As with grabbing into a non-visible bag, access is not fixed. Maps and sets produce
no (fixed) sequence!
Sorting / order
Sorting can only be established or order can only be established if the elements of a collection are comparable. Sorting and ordering does not refer to the iteration order of a collection, but to the distinguishing properties of its elements. Sorting within a collection is the bringing-into-sorting-sequence of comparable items.
Note: In the following, only the term “sorting” will be used. “order” contains too many sub-meanings and can therefore lead to confusion.
In Java there are two sorting types:
Natural
sorting
An element of a collection receives
its natural sorting via the compareTo () method in the Comparable interface.
The implementation of the interface must be done within the
element class. Examples of known natural sorts are
integers (sorted numerically) and Strings (sorted “alphabetically”), but of
course this can also be defined for any object:
public class Car implements Comparable<Car> {
public String modelName;
public LocalDate productionYear;
public Integer powerInHp;
@Override
public int compareTo(Car car) {
return this.modelName.compareTo(car.modelName);
}
}
The Car class has received its natural sorting by comparing the car model
names. The compareTo method of the String class was used.
Sorting methods such as Collections.sort
() (without parameters) automatically falls back on the natural sorting of
their elements, making it very easy to implement.
ArrayList<Car> carList = new ArrayList<Car>();
// fill carList ….
Collections.sort(carList);
However, there is only one way to determine the natural sorting. In addition, it is not possible to define a natural sort without access to the element (here Car), i.e. for all externally defined objects. If you want to sort in many different ways or have no direct access, you can use the Comparator:
Individual
sorting
To be able to sort a collection
according to your own criteria (not natural), you need a class that implements
the Interface Comparator and defines a comparison and thus a sorting variant
using the compare (obj1, obj2) method. In order to
achieve a sort by production year in the example above, you need the following
comparator:
public class ProductionYearCompare implements Comparator<Car> {
@Override
public int compare(Car car1, Car car2) {
if (car1.produtionYear.isBefore(car2.produtionYear)) {
return -1;
} else if (car1.produtionYear.isAfter(car2.produtionYear)) {
return 1;
} else
return 0;
}
}
Sorting can now be done via
Comparator<Car> yearCompare = new ProductionYearCompare();
Collections.sort(carList, yearCompare);
The new comparator was passed in the sort () method. Since Java 8, this can be realized more elegant and shorter using Lambda expressions, which sort here by horse power of Cars.
Collections.sort(carList, (car1, car2) -> car2.powerInHp – car1.powerInHp);
Which collections can be sorted?
As already mentioned, a sorting of
collections is only possible if their elements are comparable. As an elementary requirement this only applies to the Trees and the
PriorityQueue, which are in a sorted state at any time:
Tree PriorityQueue
Note: The comparability of the elements is marked here with a different proportion of red color.
Other collections must first define a comparison in order to be sortable


List sorted

Linked with comparison structure
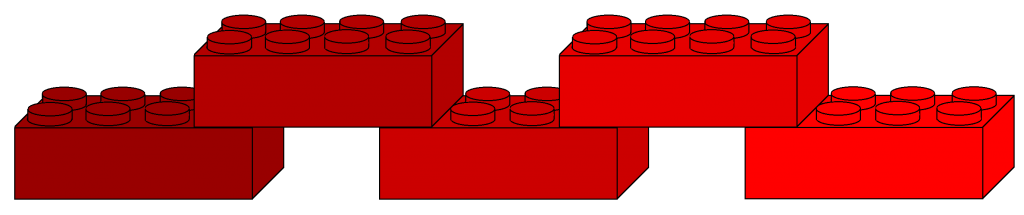
Linked sorted
As with the order, sets and maps play a special role. Comparability cannot be established (without both being embedded in a linked or tree structure). Anyway, such a procedure would not make sense, because even with existing comparability, the structures would have no fixed sequence and could not be output in sorted order.
Sorting is not possible without (fixed) sequence!
This leads us to the question of
whether there is a (fixed) sequence without sorting. This
is easy to answer: All (fixed) sequence collections without the definition of a
comparison (see Figure 1) satisfy this condition.
A (fixed) sequence without sorting is possible!
Conclusion
• The terms sequence, order and sorting could be defined in a meaningful way. A (fixed) sequence is an ordered, reproducible iteration, while sorting (or ordering) means the bringing-into-sorting-sequence of comparable items.
• With respect to collections, the sequence has to do with the underlying data structure and is thus given for all lists, all queues / deques, all linked structures and all tree structures. Sets and maps (without being embedded in other structures) have no (fixed) sequence.
• Sorting has to do with determining the comparability of the elements and is thus naturally given for Trees and Priority Queue. Other structures can establish sorting by defining a comparison, for maps and sets this is not possible (without external structuring).
• Comparability can be established either naturally – element-related via the compareTo() method – or individually – via an external comparator and the compare (obj1, obj2) method.
• A (fixed) sequence is a requirement for sorting, but the reverse is not true
